|
|
|
---- 一 个 一 般 的 数 据 模 型 由 下 列 三 要 素 组 成: 一 组 对 象 及 其 结 构、 一 组 操 作 和 一 组( 关 于 对 象 与 操 作 的) 约 束。 实 时 数 据 模 型 同 样 如 此, 其 中 的 约 束 更 突 出 地 包 括 时 间 限 制。 到 目 前 为 止, 专 门 讨 论 实 时 数 据 模 型 的 文 章 作 者 似 乎 还 未 见 到, 下 面 就 华 中 理 工 大 学 计 算 机 学 院 开 发 的 一 个 实 时 数 据 模 型 做 简 要 的 介 绍。
---- 实 时 数 据 库(RTDB) 中 包 含 下 列 三
种 类 型 的 数 据 对 象:
----1 . 映 像 对 象
---- 现 实 世 界 中 的 对 象(Real World Object,RWO) 由 传 感 器 监 视, 其 值 被 周 期 性 地 采 样, 并 写 入 数 据 库。 这 种 被 实 时 写 入 的RWO 值 的 数 据 对 象 就 称 为 映 像 对 象(Image Object,IMO), 即 一 个 IMO 就 是 一 个RWO 在 特 定 时 刻 的 映 像。 所 以, 一 个IMO 有 一 个 时 标 和 一 个 有 效 期 与 之 相 连, 它 们 分 别 对 应 于 相 关RWO 的 采 样 时 刻 和 自 此 时 刻 开 始 至 下 一 采 样 发 生 的 时 间 区 间。 一 个RWO 的 值 被 采 样 并 写 入 数 据 库 而 成 为 一IMO 的 任 务, 则 建 模 为 一 个 周 期 实 时 事 务。IMO 的 值 一 旦 记 入 数 据 库, 就 不 被 更 改, 而 将 对 应RWO 的 另 一 时 刻 值 采 样 并 写 入 数 据 库, 作 为 新 的IMO。RTDB 保 存 了 这 些IMO 的 档 储 记 录, 所 以, 对 应 的RWO 在 不 同 时 刻 的 瞬 像 是 有 效 的。 例 如, 在 时 刻t1 采 样 的 温 度 就 是 一 个IMO; 更 复 杂 的RWO 为 雷 达 所 跟 踪 的 空 中 物 体, 在 时 刻t1 到t2 间 采 样, 所 得 到 的 高 度、 速 度、 飞 行 方 向 等 都 是 不 同 的IMO。
----2 . 导 出 对 象
---- 一 个 导 出 对 象(Derived Object,DEO) 经 过 一 个 事 务 的 执 行, 由 一 组IMO 和/ 或 其 他 数 据 对 象 计 算 而 得。 显 然, DEO 也 有 时 标, 它 是 事 务 时 间, 其 有 效 期 则 应 为 导 出 它 的 多 数 据 对 象 的 有 效 之 交, 且 可 能 有 多 个 时 间 区 间 形 式。 与IMO 不 同 的 是, DEO 的 值 在 数 据 中 可 能 被 更 新, 其 档 储 记 录 可 保 存 也 可 不 保 存。
----3 . 不 变 对 象
---- 不 变 对 象(Invariant Object,INO) 是 一 个 常 数 值。 它 可 当 作 实 时 数 据 的 特 例, 其 值 不 随 时 间 而 改 变, 时 标 为 系 统 初 建 时 刻, 有 效 期 的 上 限 为" 当 前"。
---- 所 以, 一 个 实 时 数 据 对
象 为 一 个 三 元 组:d
---- 关 系 代 数 有 五 种 基 本 操 作: 选
择、 投 影、 迪 卡 尔 积、 差 和 并。 它 们 对 实 时 数 据 同 样
是 必 要 而 基 本 的, 但 其 定 义 已 不 同, 下 面 分 别 说 明:
----1 . 时 间 选 择d TC
---- 定 义 为 选 择 满 足 条 件C 的 数 据 对 象。C 可 以 是 关 于 属 性 值 的 传 统 条 件 表 达 式, 也 可 以 是 关 于 有 效 期 的 VI 时 间 条 件 表 达 式, 或 两 者 均 包 括。 被 选 取 的 数 据 对 象 的 值 和 有 效 期 均 不 变。
----2 . 时 间 投 影 πT S
---- 选 取 由S 指 定 的 属 性 值 和/ 或 有 效 期 VI, 构 成 一 个 新 的 关 系。 若S 中 未 指 定VI, 则 其 结 果 对 象 均 为 不 变 对 象, 否 则 结 果 对 象 中 具 有 相 同 值 的 对 象 可 进 行 时 间 归 并。 对 有 效 期VI 的 投 影 等 价 于 返 回 各 对 象O 的 有 效 期 的 函 数VI(O)。 例 如, " 在IBM 公 司 工 作 过 的 职 工 名 单 及 工 作 期" 可 表 示 为:
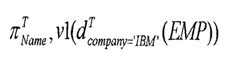
----3 . 时 间 迪 卡 尔 积XT
---- 定 义 为 两 个 数 据 对 象 在 其 公 共 有 效 期 上 传 统 的 迪 卡 尔 积。 所 以, 仅 当 两 个 对 象 的 公 共 有 效 期 不 为 空 时, 才 执 行XT, 此 时 它 相 当 于 一 个 传 统 的 迪 卡 尔 积 再 紧 跟 一 个 关 于 其 公 共 有 效 期 的d TC 的 操 作。
----4 . 时 间 差-T
---- 针 对 具 有 相 同 值 但 不 一 定 有 相 同 有 效 期 的 对 象 来 进 行。 设R,S 为 两 个 数 据 对 象 集,P=RJS 定 义 为: 对 于R 中 的 任 一Xi, 仅 当S 中 有Xj 使 得xi=xj, 且VI(xi) VI(xj) 时,xj 不 属 于P; 否 则xj 属 于P, 此 时VI(xi)=VI(xi) -VI(xj)。
----5 . 时 间 并YT
---- 首 先 定 义" 时 间 归 并" 操 作: 它 施 加 于 一 个 对 象 集, 将 其 中 所 有 具 有 相 同 值、 不 同 有 效 期 的 数 据 对 象 分 别 并 成 一 个, 其 有 效 期 为 各 相 应 有 效 期 之 并。 然 后 利 用" 时 间 归 并" 可 得 到 时 间 并 操 作, 它 等 价 于 一 个 一 般 的 并 操 作 再 紧 跟 一 个" 时 间 归 并", 这 就 意 味 着 去 掉 那 些 值 和 有 效 期 都 相 同 的 重 复 对 象。
----1 . 数 据 的 时 间 一 致 性
---- 一 个RTDB 是 相 应 现 实 世 界 的 直 接 映 像, 现 实 世 界 状 态 的 任 何 变 化 都 应 及 时 反 应 在 数 据 库 中, 换 句 话 说, 数 据 对 象 的 时 标 必 须 足 够 地 接 近 其 真 实 时 间, 使 数 据 库 的 状 态 能 反 应 现 实 世 界 的" 当 前" 状 态。
---- 令tc 表 示 系 统 的" 当 前" 时 间,tx,vix 分 别 表 示 数 据 对 象 的 时 标 和 有 效 期, 我 们 定 义x 的" 年 龄"a(x) 为:a(x)=tc - tx, 差a(x) ≤vix, 则 说x 是 外 部 一 致 的, 它 由 外 部 现 实 世 界 所 决 定 的 时 间 一 致 所 限 制。RTDB 中 的IMO 都 应 是 外 部 一 致 的。
----RTDB 中 用 来 决 策 或 导 出 新 数 据 的 一 组 数 据 称 为 一 个 相 互 集R。 它 们 应 有 一 公 共 有 效 期VIR。R 中 的 数 据 在 时 间 上 要 相 互 一 致, 我 们 定 义 两 个 数 据x,y 的 时 间 距 离d(x,y) 为|tx - ty|。 差 对 于 相 互 集R 中 任 两 数 据x,y, 有d(x,y) ≤VIR, 则 说R 是 相 互 一 致 的。 相 互 一 致 集 中 的 数 据 对 象 一 起 描 绘 现 实 世 界 某 同 一 状 态。 RTDB 中 导 出DEO 的 数 据 对 象 都 应 是 相 互 一 致 的。 不 难 看 出,INO 总 是 外 部 一 致 和 相 互 一 致 的。
----2 . 事 件 的 时 间 限 制
---- 实 时 事 务 由 事 件 驱 动, 事 件 建 模 信 息 ( 数 据) 与 时 间 之 间 的 联 系, 事 务 的 定 时 限 制 有 的 则 表 现 为 相 联 事 件 的 限 制。 有 三 种 关 于 事 件 的 时 间 限 制:
---- 两 事 件 间 的 最 大 时 距 例 如, 一 旦 一 个 飞 行 目 标 进 入 雷 达 视 野( 一 个 事 件), 目 标 识 别( 另 一 事 件) 必 须 在t1 秒 之 内 完 成。
---- 两 事 件 间 的 最 小 时 距 例 如 两 架 飞 机 的 着 陆 至 少 隔t2 秒。
---- 限 定 事 件 在 特 定 时 间 发 生 例 如 每 天7 ∶00 启 动 机 器 人。
----事 件 一 般 定 义 为 一 种 系 统 行 为 瞬 时 发 生, 也 可 以 定 义 为 短 暂 的 行 为 过 程。
----3 . 事 务 的 时 间 限 制
---- 实 时 事 务 的 定 时 限 制 有:
---- 限 定 事 务 执 行 的 开 始 例 如, 飞 机 在 距 机 场 还 有10 分 钟 的 飞 行 距 离 时, 才 开 始 着 陆 请 求。
---- 限 定 事 务 执 行 的 结 束 这 是 一 种 最 典 型 的 实 时 事 务 的 限 制, 即 事 务 的" 截 止 期"。 例 如, 飞 机 必 须 在 着 陆 的 前10 秒 放 下 着 陆 轮。
----限 定 事 务 在 指 定 期 间 执 行 例 如, 结 算 在 每 天 的24 ∶00 至0 ∶30 期 间 执 行。
----实 时 事 务 的 定 时 限 制 来 自 于 外 部 环 境 的 要 求 指 系 统 性 能 要 求 及 数 据 的 时 间 一 致 性 要 求。 它 们 与 实 时 数 据 一 样, 也 表 现 出 外 部 一 致 和 相 互 一 致 性 限 制。